Anonymous Algebraic Data Types

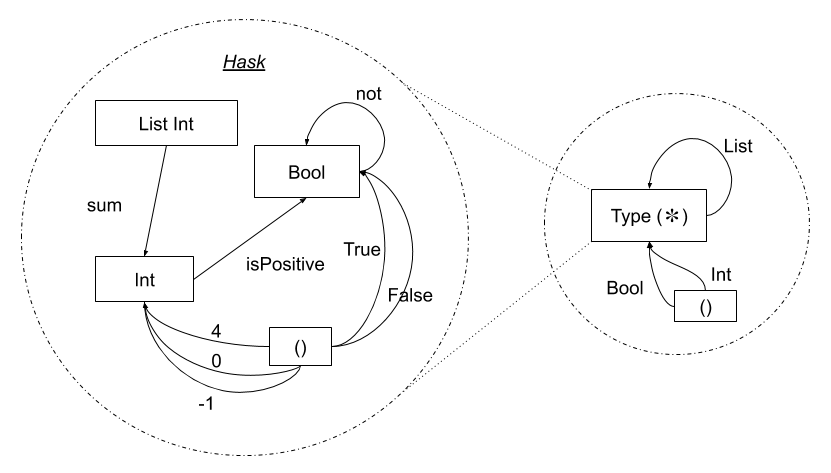
In functional programming, there is a nice symmetry between types and values. While we often think of types and values as playing different roles – the types as being the ‘objects’ and the values as being the ‘arrows’ (or the inhabitants of types) in the category of types (Hask) – we can also look at types as ‘values’ themselves, of an object called ‘Type’ (often denoted ‘*’), in a higher level category. (As illustrated in figure 1).

And in functional programming, we understand the value of values¹ (as contrasted with say objects in object-oriented programming); we know that strings as values is better than strings as objects because equality means what we expect it to, and the string has a meaning independent of time and place; similarly for more complex data structures we prefer algebraic data types whose instances are values, to classes in object oriented programming whose instances are objects that are inseparable from a pointer to a location in memory; we also treat functions as values, allowing them to be passed in as arguments or returned from other functions, increasing the power of composition and hence the modularity of our programs.

But I feel we could do more to expose the simple symmetries that allow types to be treated as values². In particular, I would like to be able to construct algebraic data types anonymously, which is not currently possible in Haskell. In Elm, algebraic data types of the ‘product’ variety can be constructed anonymously, which feels very natural, and I would like to explore how we could extrapolate this approach to all algebraic data types.

How can we think about types anonymously? For a start, for the building blocks we have the atomic (a.k.a primitive) types – Unit, Boolean, Char, String³, Int, Float. Then we need the operations that generate new types from old; there are a few different atomic type operations⁴ but in this post I am limiting the scope to just the two operations involved in constructing algebraic data types – ‘product’ and ‘sum’. Then, just like in ordinary level programming where we start with some atomic functions and we can compose them together to form infinitely many possible new anonymous functions, so too starting with these atomic types we can combine them together using these two atomic type operations, ‘product’ and ‘sum’, in any number of iterations and combinations, to form infinitely many possible new anonymous types. The set of all these types reached, which I like to call the ‘span’ of the atomic types under the product and sum operations, is precisely⁵⁶ the algebraic data types.

So far I have been a little vague on what I mean by these ‘product’ and ‘sum’ operations, and actually the details of how we choose to define them are important for being able to use them anonymously, and aren’t yet consistent across functional languages. Less vaguely, what I mean by ‘product’ and ‘sum’ in this context are I think better described by the more qualified names ‘tagged product’ and ‘tagged union’ respectively, so as to distinguish them from the ‘untagged’ versions used in mathematics (whose binary instances we are familiar with in programming as Tuple and Either respectively). Unlike in mathematics where we only care about the structures up to isomorphism, in programming it is helpful if the ‘tag’ names are included as intrinsic parts of the operations. But in every other respect the constructions of the corresponding ‘tagged’ types can be thought of very similarly – as universal constructions in category theory that are dual to each other (which is a special kind of symmetry that just means the constructions are the same but with the arrows the opposite way round), as illustrated in figure 2.

Note that these definitions are slightly different to how ‘product’ and ‘sum’ are implemented in Haskell; for example in the sum operation above each of the component tags can only take one type argument⁷, unlike in Haskell (and Elm) where each of the component tags can take any number of type arguments; also order of the types is not an intrinsic part of either the product or sum operations above, unlike in Haskell where the product is defined by a curried data constructor which takes the types in order and ‘record syntax’ is just the syntactic sugar. I think these differences are without loss of generality⁸, and the reason I like the above definitions is that they make the product and sum operations exactly dual to each other.

There is still more that needs to be detailed though for these constructions to be able to be used anonymously; we require that the functions corresponding to each tag (one for each arrow in the diagram figure 2), which we need as building blocks for defining functions to and from algebraic data types, can also exist anonymously. For this to work, I think they need to be automatically namespaced to the type itself both for product and sum types, unlike in Haskell where the functions in both cases are created in the global namespace⁹; in other words the type needs to double up as a ‘module’ containing a function for each ‘tag’ (so for example if Car is a type synonym for the product type {make: String, model: String, year: Int}, then Car.make is the fully qualified name, in any namespace, of the function make: Car -> String).¹⁰ This is easier said than done, as it would lead to awkward name clashes in Haskell imports for modules to be allowed to contain types of the same name that can also be used as ‘modules’, without making changes to the way modules and imports work.

In this post I have presented how I like to think of algebraic data types, and highlighted where this view differs from how they are implemented in Haskell, (ignoring any of the potentially awkward practical considerations of integrating it into Haskell). In this view, algebraic data types can be summarised as the ‘span’ over the atomic types of two dual atomic type operations, ‘product’ and ‘sum’, each of which can build a new type given any ‘map’ of arbitrary tag names to existing types. The advantages of viewing algebraic data types in this way, are that we can see the intrinsic nature of them as anonymous ‘values’ in a type level category, and also we can appreciate the duality of the two atomic type operations, ‘product’ and ‘sum’, which generate them.