The Fair Exchange Rate

Written 2021

In ‘What Makes Human Unique?’, I thought about the role exchange could have played as a significant driving force in human evolution. While I was thinking about this, and in particular how calculation skills may be relevant to exchange, it became natural to ask whether calculation could ever have been useful for determining the fair exchange rate? And more generally, is it even possible to calculate the fair exchange rate?

After a few days I concluded that it is not practical to calculate a fair exchange rate in general. And so while humans do have an ability to calculate, which is useful for arbitrage, it has not been needed for agreeing the fair price of an exchange. This fact that prices aren’t determined by calculation isn’t a new result at all – we already know in Economics that prices are determined by supply and demand (or monopolies¹), and in a more direct market by bartering – however it’s still illuminating to understand why a fair exchange rate is not even possible to calculate in practice, so I’ll share what I’ve learnt in attempting to find it.

The discussion

To set the context, we need to understand what it is that makes a trade mutually beneficial in the first place. It turns out to not need much – whenever two parties value two products differently, there can be mutual benefit from exchange. So for example² if I value gold twice as much as silver, say because I live near a silver mine and it takes me twice as long to extract gold as silver, and you value silver twice as much as gold because you live near a gold mine and it takes you twice as long to extract silver as gold, then we can mutually benefit by me trading my silver with your gold. Notice that it doesn’t matter at all who is actually more efficient at extracting gold and who is more efficient at extracting silver – it could be the same party that is more efficient at both – all that matters is that the relative value of your gold to my silver is higher for me than it is for you³. This slightly counterintuitive result, that you don’t have to be the best at a trade for people to benefit from trading with you, is Ricardo’s Law of Comparative Advantage⁴. As for the exchange rate, since I value \(\text{silver}:\text{gold}\) at \(2:1\) and you value \(\text{silver}:\text{gold}\) at \(1:2\), the trade will be mutually beneficial at any exchange rate strictly between these two ratios.

Generalising from this example, suppose there are two parties producing two different products – Party \(A\) produces \(\alpha\) and Party \(B\) produces \(\beta\) – and suppose Party \(A\) values the products \(\alpha:\beta\) at \(1:x\) and Party \(B\) values the products \(\alpha:\beta\) at \(1:y\)⁵, where \(x < y\); then the parties can mutually benefit by Party \(A\) exchanging \(\alpha\) with \(\beta\) from Party \(B\), at any exchange rate strictly in between \(1:x\) and \(1:y\).

The question is then, out of this range of exchange rates, what exchange rate should be chosen – what is the fair exchange rate? Informally, it makes sense to pick something in the middle, but by what average – the arithmetic mean, the geometric mean, some other mean…?

In the case of the gold and silver example, if we assume that I value silver the same as you value gold, because say it takes me the same time to extract silver as it takes you to extract gold, then by the complete symmetry of the situation we can deduce that the fair exchange rate has to be an exchange rate of \(1:1\), which is the geometric mean of \(2:1\) and \(1:2\).

However, I can also find an example where the geometric mean can’t be the fair exchange rate. Consider the example of exchanging a product for money. For concreteness let’s say the product is an Apple MacBook laptop. Apple knows the minimum amount of money they would be willing to sell the laptop and still make a profit, and I know the maximum amount of money I would be willing to spend on the laptop and still feel like it’s value for money. If the amount of money I am willing to spend is more than Apple is willing to sell it for, then there can be mutual benefit in the exchange, and common sense says that the fairest exchange rate for \(\frac{\text{MacBook}}{\$}\) would be the arithmetic mean of the lowest price Apple is willing to sell (how Apple values \(\frac{\text{MacBook}}{\$}\)) and the highest price I would be willing to buy (how I value \(\frac{\text{MacBook}}{\$}\)).

What is it that’s different about the second example that makes the fair exchange rate the arithmetic mean as opposed to the geometric mean? The key difference is that in the second example, one side of the exchange is money. Although money can be thought of as a product to be exchanged just like any other product, it’s special because it’s value is exclusively in what it can be exchanged for, and this is the same for everyone. Therefore we can say in absolute terms that the value of one laptop to Apple is the same as the value to me of the minimum amount of money Apple is willing to sell it for. In the case of gold and silver though, neither gold nor silver has the same absolute value to me as it does to you, and instead it is the absolute value of silver to me that is equal to the absolute value of gold to you (because that was the assumption we made to make the situation symmetrical).

So it seems like for a given exchange, the fair exchange rate depends also on an absolute comparison of how each party values the exchanged products. As we said, this is possible to do with money because what I can buy with a given amount of money is exactly the same as what you can buy with the same amount of money⁶. So I think in a market with money, the calculation is theoretically possible. Though I don’t think it would have been used in practice. For a start, in a modern market with money, agreement of a pairwise exchange rate is less relevant as prices are not set for each exchange but rather the market as a whole. Even if prices are not fixed and are agreed on a pairwise basis, there is no incentive to honestly share the minimum rate you are willing to exchange for until absolutely necessary, so bartering would be the natural method to determine the price. In a market without money, I don’t think it’s even theoretically possible to determine a fair exchange rate, as does it even make sense to absolutely compare how much I value something with how much you value something⁷?

The maths

Even though an absolute comparison of value is impossible to determine in practice (especially in a world without money), it doesn’t stop us doing some algebra with it, to theoretically determine the precise relationship between absolute values and the fair exchange rate in the general case.

Suppose:

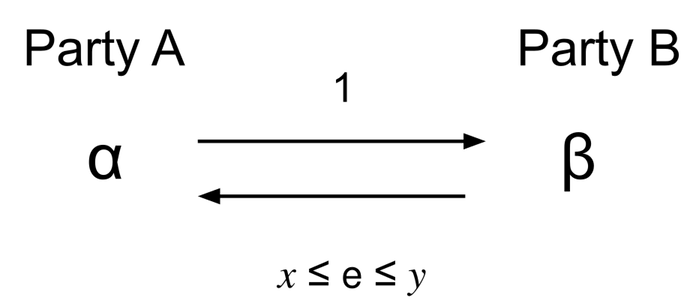
Party \(A\) specialises in producing \(\alpha\) and Party \(B\) specialises in producing \(\beta\).
Party \(A\) values \(\alpha:\beta\) at \(1:x\).
Party \(B\) values \(\alpha:\beta\) at \(1:y\).
Using subscripts to denote the value of a product to a particular party, we can write this in equations as:
\(x = \frac{\alpha_A}{\beta_A}\), \(y = \frac{\alpha_B}{\beta_B}\).

We assume that \(x < y\), so that the trade is viable. Then \(A\) and \(B\) can trade at an exchange rate \(e\), yet to be calculated, where \(x \leq e \leq y\).

Let \(v\) be such that, in absolute terms, the value of \(\alpha\) to \(A\) is \(v\) multiplied by the value of \(\beta\) to \(B\). As an equation: \(v = \frac{\alpha_A}{\beta_B} = x \frac{\beta_A}{\beta_B} = y \frac{\alpha_A}{\alpha_B}\).

Then:

For every \(\alpha\) transferred from Party \(A\) to Party \(B\), \(e * \beta\) is transferred from Party \(B\) to Party \(A\).

From the point of view of Party \(A\), the net gain in the transaction is \(e * \beta_A – \alpha_A = \frac{e}{x} * \alpha_A- \alpha_A = (\frac{e}{x} – 1) \alpha_A\).

From the point of view of party \(B\), the net gain in the transaction is \(\alpha_B – e * \beta_B = y \beta_B – e \beta_B = (y – e) \beta_B\).

For this to be a fair exchange, the net gains are equal so
\((y – e) \beta_B = (\frac{e}{x} – 1) \alpha_A\).

Substituting in \(\alpha_A = v \beta_B\),
\(y – e = (\frac{e}{x} – 1) v\).

Rearranging for \(e\) in terms of \(v\), \(x\) and \(y\), we conclude:

\(e = \frac{v x + x y}{x + v} = x (1 + \frac{y-x}{v+x})\)

Interesting special cases:

There are some interesting special cases to this which relate to the previous examples.

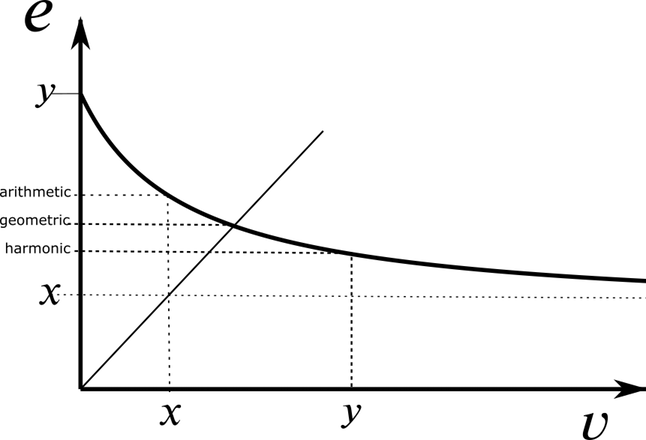
If \(v = x\) then \(e = \frac{x + y}{2}\) (the arithmetic mean of \(x\) and \(y\))
If \(v = y\) then \(e = \frac{2}{\frac{1}{x} + \frac{1}{y}}\) (the harmonic mean⁸ of \(x\) and \(y\)).
The geometric mean, \(e = \sqrt{x y}\), occurs when \(v = e\).

Then there are also the limit cases:
As \(v \rightarrow 0\) then \(e \rightarrow y\) (the upper boundary value)
As \(v \rightarrow \infty\) then \(e \rightarrow x\) (the lower boundary value)

Incidentally, these examples also provide a nice way to prove the AM-GM inequality⁹.

The conclusion

In conclusion, the fair exchange rate doesn’t exist in general because it depends on a property – the absolute comparison between how each party values the exchanged products – which can’t be objectively measured. So while exchange is always mutually beneficial (at least to the extent that each party knows their own best interest), there is not always a way to objectively determine if it is fair.