Natural numbers are used for counting discrete collections of objects; addition corresponds to combining collections and multiplication to making copies of a collection. For example, when the objects are eggs, you know what I mean when I say I have \(3\) eggs, you know that if I add \(9\) eggs to \(3\) eggs I have \(3 + 9 = 12\) eggs, and if I have \(5\) packets each with a dozen \((12)\) eggs, I have a total of \(5 \times 12 = 60\) eggs. Real numbers just do not make sense in this context – I think you would have a pretty hard time picturing \(-1\) egg, and similarly I don’t think there is an obvious way to make \(\frac{1}{2}\) a bracelet make sense.
Instead, real numbers should be thought of as the language for continuous space. For example real numbers can be used to label all the points of a line, and pairs of real numbers (or complex numbers) to label all the points in the plane.
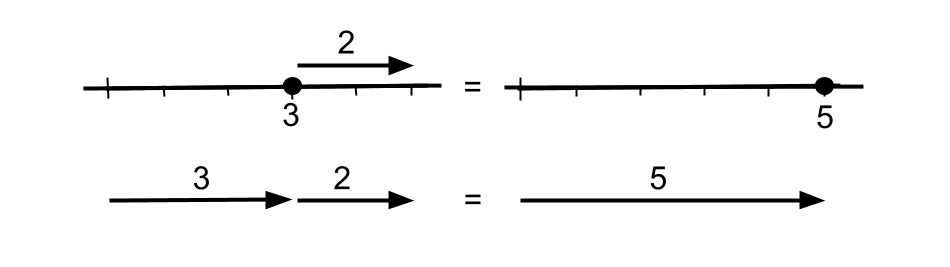
But this isn’t the whole picture of real numbers, because for example you can add any two real numbers but it does not make sense to add together two points on a line. This leads to the second way to visualise real numbers as vectors, which act on points by translations. A vector can be represented by an arrow. It makes sense to add a vector to a point, or to add two vectors, as illustrated in Figure 1.
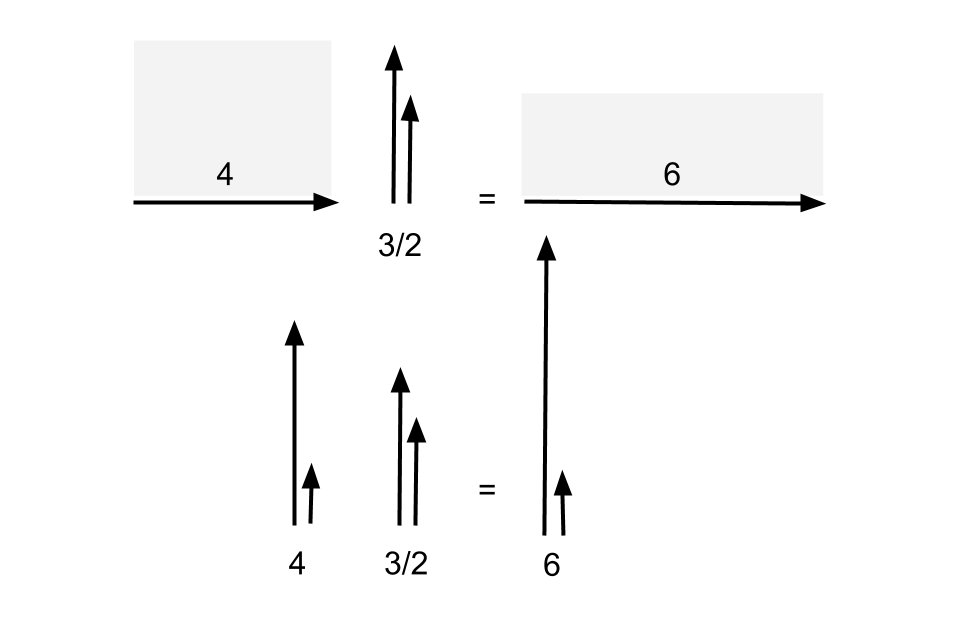
There is one final way to visualise real numbers, as scalars which act on vectors by enlargements. You probably have quite an intuitive feel for what scalars are, but there isn’t such a neat representation for scalars as there was for vectors (which can be represented as arrows); the best you can do with a scalar is represent it as a ‘ratio’ of two vectors (just as a vector could also be represented as a ‘difference’ of two points instead of an arrow). Scalars is the context in which multiplication makes sense; it makes sense to multiply a vector by a scalar, or multiply two scalars, as illustrated in Figure 2.
These three perspectives of real numbers are very integrated – scalars act on vectors which act on points. In the language of functions and composition (category theory), vectors are functions of points, scalars are functions of vectors (so second order functions of points), addition can be interpreted as either application of vectors to points, or composition of vectors, and similarly multiplication is application of scalars to vectors, or composition of scalars.
Scalars are in some sense the ‘pure’ real numbers, because every real number corresponds directly to a scalar without any arbitrary choices needing to be made. To identify real numbers with vectors however, it is necessary to choose a special unit vector \(\underrightarrow{1}\), and then all vectors can be represented by \(\underrightarrow{x} := x \underrightarrow{1}\) for some scalar \(x\). To identify real numbers with points, we need to further choose a special origin point \(\underset{\cdot}{0}\), and then all points on the line can be represented by \(\underset{\cdot}{x} := \underrightarrow{x} 0 = x \underrightarrow{1} \underset{\cdot}{0}\) for some scalar \(x\). (Here I am using Haskell’s notation for function application, where function application is represented by a space and is left associative).
Having said all this, there are clearly similarities between the natural numbers and the real numbers, for a start the natural numbers are ‘contained’ in the real numbers. What they have in common is precisely this structure of second order functions acting on first order functions acting on objects in a ‘nice’ way. The difference is that in the case of real numbers the scalars act on units of ‘space’ which are divisible and have direction, whereas in the case of natural numbers the scalars can act on objects which are indivisible and do not have a meaningful direction. In terms of the abstract structure this means that in the real numbers all inverses (multiplicative and additive) exist, whereas in the natural numbers they don’t.
 RSS - Posts
RSS - Posts
I guess there is something more general that can be learned from this. When X is a subset of Y it makes it feel as though Y is more general than X, in terms of its applications. But actually the reverse is true – the set of interpretations of X is a superset of the set of interpretations of Y because every interpretation of Y can be restricted to an interpretation of X but not vice versa.